* 인공지능 강의 정리용
1. 지식 표현
데이터 피라미드 : 데이터 → 정보 → 지식 → 지혜 순
- 데이터 : 특정 분야에서 관측된 가공되지 않은 것, 오류나 잡음 포함 가능
- 정보 : 데이터를 가공하여 어떤 목적이나 의미를 갖도록 한 것
- 지식 : 정보를 취합하고 분석하여 얻은 대상에 대해 사람이 이해한 것
- 지혜 : 경험과 학습을 통해서 얻은 지식보다 높은 수준의 통찰
cf) white noise : 잡음 없을 시 깨끗한 데이터 인식 어려울 수 있음.

지식
경험이나 교육을 통해 얻어진 전문적인 이해와 체계화된 문제 해결 능력
특정 주제나 분야에 대한 이론적/실제적 이해. 현재 알려진 사실과 정보 모음
- 절차적 지식 : 문제 해결의 절차 기술
- 선언적 지식 : 어떤 대상의 성질, 특성이나 관계 서술
컴퓨터를 통한 지식 표현의 경우 프로그램이 쉽게 처리할 수 있도록 정형화된 형태로 지식을 표현 (수치, 규칙, 프레임, 논리 등)
2. 규칙
조건부의 지식을 표현하는 if-then 형태의 문장
규칙 획득 및 표현
대상, 속성, 행동 또는 판단의 정보 추출 (if 배가 고프다 then 밥을 먹는다)
- if : 조건부, 주어진 정보나 사실에 대응될 조건
- then : 결론부, 조건부가 만족될 때의 판단이나 행동
규칙의 구성
- 조건부 : 둘 이상의 조건을 AND / OR로 결합하여 구성 가능 (if A or B then C / if A and B then C)
- 결론부 : 여러 개의 판단 또는 행동 포함 가능 (if 조건 then (A and B and C))
- 휴리스틱 : 경험적인 지식을 표현 (실행한 결과를 통해 새로운 지식을 update)
3. 프레임
특정 객체 또는 개념에 대한 전형적인 지식을 슬롯의 집합으로 표현하는 것
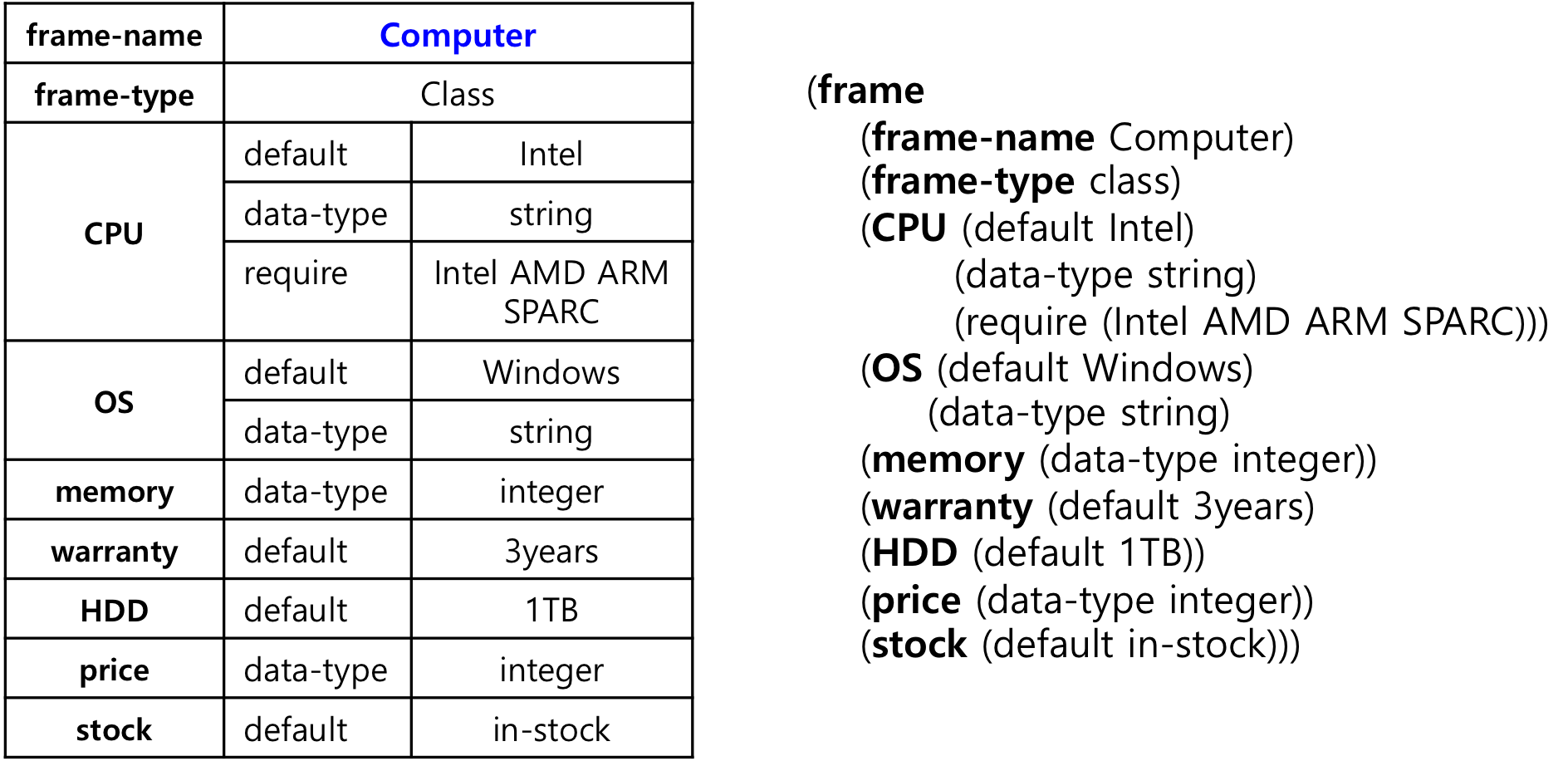
프레임의 구성 요소
슬롯
객체의 속성을 기술, 슬롯 이름과 슬롯 값으로 구성
슬롯 값 : 복수 개의 패싯(이름-값)과 데몬(실행조건-이름)으로 구성
패싯
속성에 대한 부가적인 정보 지정 위함, 패싯 이름 ─ 패싯 값 쌍으로 구성
- value : 속성값 (수, 문자열, ...)
- data-type : 속성값의 자료형
- default : 속성값이 주어지지 않았을 때의 초기값
- require : 슬롯에 들어갈 수 있는 값이 만족해야 할 제약조건
데몬
지정된 조건을 만족할 때 실행할 절차적 지식, 데몬 실행조건 - 데몬 이름 쌍
데몬의 실행조건 예시
- if_needed : 슬롯 값 알아야 할 때 (사용하려고 할 때)
- if_added : 슬롯 값이 추가될 때
- if_removed : 슬롯 값이 제거될 때
- if_modified : 슬롯 값이 수정될 때
프레임의 종류
- 클래스 프레임 : 클래스에 대한 정보 표현
- 인스턴스 프레임 : 특정 객체에 대한 정보 표현
프레임 계층구조
- 상위 프레임 : 클래스를 나타냄
- 하위 프레임 : 하위 클래스 프레임 또는 상위 프레임의 객체, 상위 프레임을 상속받음 → 같은 특성 공유
프레임과 규칙을 결합한 지식 표현
프레임은 특정 개념이나 대상에 대한 속성을 표현 → 관련 속성들을 하나로 묶어서 관리함
규칙을 사용하여 조건적인 지식 표현 → 데몬에 규칙 사용 / 규칙의 조건부나 결론부에 프레임 사용
대부분의 규칙 기반 시스템에서 객체의 개념을 사용 → 객체의 표현에 프레임을 사용 가능
프레임과 클래스&객체 간 구분
- 클래스&객체 : 소프트웨어 개발에 있어 모듈화, 재사용성, 유지보수의 용이성을 고려함. 정보 접근에 대한 제한 메커니즘
- 프레임 : 사람이 특정 대상에 갖는 지식의 표현을 목표, 슬롯의 특정 상황에 따라 데몬이 자동 호출되는 개념
4. 논리
말로 표현된 문장들에 대한 타당한 추론을 위해 기호를 사용해 문장을 표현, 기호의 조작을 통해 문장의 참/거짓을 판정
삼단논법 → 명제 논리 → 술어 논리
4.1 명제 논리
명제
참, 거짓을 분명하게 판정할 수 있는 문장. p, q 등과 같은 기호로 표현
명제 기호의 진리값을 사용해 명제들에 의해 표현되는 문장들의 진리값 결정 → 문장 자체의 내용보다 진리값에만 관심
- 기본 명제 : 하나의 진술로 이루어진 최소 단위의 명제
- 복합 명제 : 기본 명제들이 결합되어 만들어진 명제
명제 논리의 구문
논리식
명제를 기호로 표현한 형식, 명제기호와 논리기호를 사용하여 구성
| 논리 기호 | 이름 | 논리식 | 의미 |
| ¬ | 부정 (negatation) | ¬P | not P |
| ∨ | 논리합 (disjunction) | P∨Q | P or Q |
| ∧ | 논리곱 (conjunction) | P∧Q | P AND Q |
| → | 함의 (implication) | P→Q | if P then Q |
| ≡ | 동치 (equivalence) | P≡Q | (P→Q)∧(Q→P) |
- 리터럴 : 명제 기호 P와 명제 기호의 ¬P 부정, 즉 기호 그 자체
- 절 : 리터럴들이 논리합으로만 연결되거나 논리곱으로 연결된 논리식
- 논리곱 정규형 : 논리합 절들이 논리곱으로 연결되어 있는 논리식
- 논리합 정규형 : 논리곱 절들이 논리합으로 연결되어 있는 논리식
| 논리곱 절 | (P∨Q∨¬R) |
| 논리합 절 | (P∧Q∧¬R) |
| 논리곱 정규형 | (P∨Q∨¬R)∧(¬Q∨R∨S)∧(P∨R∨S) |
| 논리합 정규형 | (P∧Q∧¬R)(¬Q∧R∧S)(P∧R∧S) |
정형식
문법에 맞는 논리식으로 다음과 같은 조건을 만족해야만 맞는 문법의 논리식임.
- 진리값 T, F와 명제 기호들 P, Q, R, ... 은 정형식이다.
- p와 q가 정형식이면 논리 기호를 사용하여 구성되는 논리식들도 정형식이다.
- 1과 2에 의해 정의되는 논리식만 정형식이다.
명제 논리의 의미
진리표
논리기호에 따라 참, 거짓 값을 결합하는 방법을 나타낸 표
| P | Q | ¬P | P∨Q | P∧Q | P→Q | P≡Q |
| F | F | T | F | F | T | T |
| F | T | T | T | F | T | F |
| T | F | F | T | F | F | F |
| T | T | F | T | T | T | T |
이 때 논리식의 진리값을 결정하는 것 : 논리식의 해석, 이 때 먼저 명제 기호의 진리값 결정 필요
명제 기호에 명제를 대응시키고 해당 명제의 진리값을 결정, 대응된 명제를 명제기호의 외연 또는 의미라 함
논리식의 모델
논리식의 명제기호에 참값 또는 거짓값을 할당한 것 ( (P∧Q) : P=True, Q=False )
모델이 주어지면 진리표를 사용해 논리식의 해석이 가능
n개의 명제 기호가 논리식에 사용된다면 각각 T/F 값을 가질 수 있으므로 총 2^n개의 모델이 존재
타당한 논리식
모든 가능한 모델에 대해 항상 참인 논리식 → 항진식
↔ 항위식 : 모든 가능한 모델에 대해 항상 거짓이 되는 논리식
충족가능한 논리식
참으로 만들 수 있는 모델이 하나라도 있는 논리식. (결론은 항상 참)
ex) (P∧¬Q)∧(Q∨¬R) = (P and (not)Q) and (Q or (not)R))에서 P=T, Q=T, R=F
충족불가능한 논리식
참으로 만들 수 있는 모델이 전혀 없는 논리식
(ex : 항위식)
동치관계의 논리식
어떠한 모델에 대해서도 같은 값을 갖는 두 논리식

동치관계를 이용한 논리식의 변환
동치관계를 이용해 임의의 논리식을 논리곱 정규형과 같은 정형식으로 변환 → 복잡한 논리식의 단순화

논리적 귀결
Δ : 정형식의 집합 ( Δ = {P, P→Q} )
ω : 정형식 ( ω = P )
Δ ⊨ ω (Entailment)
Δ에 있는 모든 정형식을 참으로 만드는 모델이 ω를 참으로 만듬
= Δ는 ω를 논리적으로 귀결한다. = ω는 Δ를 논리적으로 따른다. = ω는 Δ의 논리적 결론이다.
추론 : 참으로 알려진 Δ로부터 알려지지 않은 참인 ω를 찾는 것.
명제 논리의 추론
- 귀납적 추론 : 관측된 복수의 사실들을 일반화하여 일반적인 패턴 또는 명제를 도출하는 것
- 연역적 추론 : 참인 사실들 또는 명제들로부터 새로운 참인 사실 또는 명제를 도출하는 것
논리에서의 추론 : 함의 (→) 의 논리적 관계를 이용하여 새로운 논리식을 유도하는 것. (p→q)
추론규칙
참인 논리식들이 논리적으로 귀결하는 새로운 논리식을 만들어내는 기계적으로 적용되는 규칙
- 긍정 논법
- 부정 논법
- 삼단 논법
추론 규칙의 정당성 : 추론 규칙이 만들어 낸 것은 항상 참이다.
추론 규칙의 완전성 : 주어진 논리식들이 논리적으로 귀결하는 것들은 추론 규칙이 찾아낼 수 있다.
정리 증명
공리를 이용해 정리가 참인 것을 보이는 것.
- 공리 : 추론할 때 참인 것으로 주어지는 논리식
- 정리 : 공리들에 추론 규칙을 적용하여 얻어지는 논리식
- 구성적 증명 : 공리들에 추론규칙을 적용해 증명을 만들어 보이는 증명
- 논리융합 반박 : 증명할 정리를 부정한 다음 논리융합 방법을 적용하여 모순이 발생하는 것을 보여 정리가 참임을 증명

명제 논리의 지식표현
문장으로 표현된 지식으로부터 기본 명제를 추출 → 각 명제에 명제 기호 부여
→ 기본 명제들의 논리적 연결 관계를 참고하여 대응되는 명제 기호들을 논리 기호로 연결하여 논리식 구성
명제 논리로 표현된 지식에 대한 추론은 명제의 의미와는 무관, 기호 연산만을 통해 추론 수행
![[인공지능] 지식표현과 추론 Part 1](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FxRrVZ%2FbtrzmkwBzlP%2FAAAAAAAAAAAAAAAAAAAAAC01LPofuDA-n1Nt216STaeGzsQ2uStWQgk6YKmeorUM%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DRNj1kOflc3ULfYhOjF%252B7RhntoRQ%253D)